1 Getting Started

---

1.1 Introduction

The spatial arrangement within cities is at an elementary level, composed of streets, buildings, infrastructure and leasure areas. Space is connected by physical networks configured to support various forms of transportation such as railway lines, footpaths and roads. The variable efficiency of such networks impacts the times to travel between connected locations and influence future developments by impacting the way in which people use space.

Complex network attracts increasing attention in many fields and analytics tools offer tool for empirically investigating the structure and evolution of network structures. Since the latter period of the 20th century, there has been an explosion of research into the structure and function of complex networks.

In this chapter, you will be introduced to two main topics that will ground all the following chapters of the book: 1. network and 2. forecasting techniques for spatial network data. To understand the fundamentals of these two broad topics, the basic concepts and terminology of networks are introduced. Particular attention is paid to spatial networks in order to limit the scope of the review. Methods for forecasting network data are subsequently introduced.

1.2 Network

1.2.1 Network: fundamentals

The network science literature provides a diverse range of tools and techniques for analysing and enhancing our understanding of the structure and large-scale statistical properties of networks. A network is a set of discrete items, called nodes, with connections between them, called edges. A network is typically represented as a graph G = (N, E), with a set of N nodes and E edges. In road network, each intersection is a node and the road segments between intersections are edges.

A bimodal network (also called bipartite network) is one which connects two varieties of things, whereas unimodal (or unimode) network connects nodes with same characteristics (see figure 1.1)

Figure 1.1: Topology of networks (source: Wasserman and Faust 1994)

To analyse and model a network process, a network is represented mathematically by a matrix describing the list of adjacency edges of incoming and outgoing vectors (Figure 1.2).

Figure 1.2: The London Congestion Analysis Project road links

In broad terms, networks can be divides into four categories (see Newman 2003):

• Social Network: a set of people (or animals) with associations between them. The core foundation of social network analysis is to understand the effect of social networks on social processes as for example friendship networks, a business network or even animal interactions.

• Information Network: networks of information flow. Pieces of information are stored at the nodes. The edges between nodes signify connections between information sources (for example academic citation networks and the world wide web).

• Biological Network: networks of biological systems, where the nodes are biological entities and the edges are connections between them (for example, metabolic networks, neural networks and food webs).

• Technological Network: man-made, physical networks, designed to transport people, resources or commodities as the network of streets and roads, railways and airlines.

The scales of analysis of a network is usually decomposed in three different levels of description as presented in figure 1.3. Network theory has long been applied to transportation systems studies which seek to understand the dynamics of physical networks designed to transport people and to evaluate impacts on transportation system performance (Xie and Levinson 2007).

Figure 1.3: Network structures (source: Borgatti and Johnson 2013).

1.2.2 Road Network and Travel Time as a Variable for Transportation

Road network is among the most recognisable and studied types of network. Traffic on urban networks is fundamentally different to traffic on highways, primarily because it is interrupted by traffic signals at intersections. When flow volume within a network nears capacity, mobility can slow or stop depending on the exact nature of these constraints.

The underlying factor that determines the speed of the traffic stream on both highways and urban roads is interaction between the demand for road space and the supply of road space, known as capacity. Congestion is characterised by slow moving stop and go traffic and is very frustrating and costly for road users.

Travel time (TT) is one of the most important variables in transportation. Accurate travel-time prediction is crucial to the development of transportation systems and advanced traveler information systems. Travel time prediction in conjunction with traffic network analytics fosters route-guidance systems and supports transportation planning and operations.

Some of the common applications of traffic network analysis are listed on table 1.1.

Table 1.1: Traffic network analysis applications (source: Ordnance-Survey 2017)

Application	Description
Catchment-area analysis	Command and control for emergency services
GIS analysis, indexing and mapping	Highway design, planning and engineering
In-vehicle navigation and guidance	Derivation of street gazetteers
Logistics management	Real-time traffic control
Road and highway maintenance	Road-user charging schemes
Route planning and vehicle tracking	Scheduling and delivery
Site location	Traffic management

The study of road network structure predates the field of complex networks and has long been of interest due to its inherent impact on transportation system performance. Forecasting models of network data have traditionally focussed on time series approaches. In such approaches, the network structure is ignored and each of the time series at the nodes is forecast independently. More recent approaches use network structures to construct spatio-temporal models that capture the spatio-temporal dependency between locations where network data are observed. Increasingly, researchers and practitioners are turning towards less conventional techniques, often with their roots in the machine learning (ML) and data mining communities, that are better equipped to deal with the heterogeneous, nonlinear and multi-scale properties of large scale network datasets.

For the forecast of urban network, observations are made at regular intervals using traffic static sensors, such as loop detectors or automatic number plate recognition (ANPR) cameras, which measure traffic conditions at a fixed point or along a section of road called a link. These sensors are distributed across the network, and when considered together, form a space time series that describes the network process (for instance, transportation systems, the internet and electrical grids).

The majority of the literature on traffic forecasting focuses on data-driven approaches. In such approaches, statistical relationships are extracted from historical data, and used to forecast future traffic conditions using information about the current traffic conditions.

Spatial network data combines the challenges of modelling time series and spatial series, which are autocorrelation, nonstationarity, heterogeneity and nonlinearity (see Haworth 2013). The choice of method depends on the dataset and an explanatory spatio-temporal data analysis must be done to better understand the characteristics of the data.

Table 1.2: Forecast of traffic data (source: Haworth 2013)

Problem	Variable	Description
Traffic flow forecasting	Flow (q)	The rate at which vehicles pass a point during a given period.
Travel time forecasting	Travel time (TT)	The time taken to travel between two fixed points.

---

1.3 Forecasting

Forecasting is a technique that uses historical data as inputs to make informed estimates that are predictive in determining the direction of future trends. A good definition is ofered by Hyndman and Athanasopoulos (2018).

Forecasting: is about predicting the future as accurately as possible, given all of the information available, including historical data and knowledge of any future events that might impact the forecasts. (Hyndman and Athanasopoulos 2018)

1.3.1 Space-time Series Forecasting

A time series is a set of observations on quantitative variables collected over time. In conjunction with a spatial component the series turns out to be a space-time series of values for a quantitative variable over time. Most businesses keep track of a number of time series and geographic information science also rely on data series to forecast environmental risk, weather forecast, land-cover changes over time and route network forecast.

There are many forms to predict the behaviour of a dependent variable using one or more independent variables that are believed to be related to the dependent variable in a causal fashion. Although we can sometimes use regression models to predictive analysis, its is not always possible to do so. For example, if we do not know which causal independent variables are influencing a particular time series variable, we cannot build a regression model. And even if we do have some idea which causal variables are affecting a time series, there might not be any data available for those variables. Moreover, even if the estimated regression function fits the data well, we might have to forecast the values of the causal independent variables in order to estimate future values of the dependent (time series) variable.

That said, it might be difficult or even undesirable to forecast time series data using a regression model. In these cases, it is advisable to use a time series forecasting method in which we analyse the past behaviour of the time series variables in order to predict its future behaviour (for further details and examples of forecasting methods, we recommend Hyndman and Athanasopoulos 2018). The predictability of an event depends on several factors:

• how well we understand the factors that contribute to it;
• how much data is available;
• whether the forecast can somehow affect the process that is being forecast.

Techniques that analyse the past behaviour of a time series variable to predict the future are referred to as extrapolation models.

The goal of an extrapolation model is to identify a function \(f()\) that produces accurate forecasts of future values of the time series variable.

Many methods have been developed to model time series data. A common approach involves trying several modeling techniques on a given data set and evaluating how well they explain the past behavior of the time series variable. The most used accuracy measures are the mean absolute deviation (MAD), the mean absolute percent error (MAPE), the mean square error (MSE), ant the root mean square error (RMSE).

In each of these formulas \(Y_i\) represents the actual value of \(i^{th}\) observation in the time series and \({\hat {Y_{i}}}\) is the forecasted value for this observation. These quantities measure the differences between the actual values in the time series and the predicted, or fitted, values generated by the forecasting technique. These quantities are defined as follows:

\[\begin{equation} {\displaystyle \operatorname {MAD} ={\frac {1}{n}}\sum _{i=1}^{n}|Y_{i}-{\hat {Y_{i}}}|.} \tag{1.1} \end{equation}\]

MAD (1.1) is the average of the absolute deviations or the positive difference of the given data and that certain value (generally central values). It is a summary statistic of statistical dispersion or variability.

\[\begin{equation} {\displaystyle {\mbox{MAPE}}={\frac {100\%}{n}}\sum _{t=1}^{n}\left|{\frac {Y_{i}-{\hat {Y_{i}}}}{Y_{i}}}\right|} \tag{1.2} \end{equation}\]

The difference between \(Y_i\) and \({\hat {Y_{i}}}\) is divided by the actual value \(Y_i\) again. The absolute value in this calculation is summed for every forecasted point in time and divided by the number of fitted points n. Multiplying by 100% makes it a percentage error.

\[\begin{equation} {\displaystyle \operatorname {MSE} ={\frac {1}{n}}\sum _{i=1}^{n}(Y_{i}-{\hat {Y_{i}}})^{2}} \tag{1.3} \end{equation}\]

That is, MSE (1.3) is the mean of \({\displaystyle \left({\frac {1}{n}}\sum _{i=1}^{n}\right)}\) of the squares of the errors \({\displaystyle (Y_{i}-{\hat {Y_{i}}})^{2}}\)

\[\begin{equation} \operatorname{RMSE} = \sqrt{MSE} \tag{1.4} \end{equation}\]

The RMSE (1.4) represents the square root of the differences between predicted values and observed values. These deviations are called residuals when the calculations are performed over the data sample that was used for estimation of prediction errors when computed out-of-sample.

1.3.2 Forecasting Models of Spatial Network Data

Forecasting models of network data have traditionally focussed on time and flow series approaches. In such approaches, the network structure is ignored and each of the time series at the nodes is forecast independently.

Because of the many factors that determine urban traffic, it is very difficult to model traffic as a physical process. The majority of the literature on traffic forecasting focuses on data-driven approaches. In such methods, statistical relationships are extracted from historical data, and used to forecast future traffic conditions.

Observations of a space-time process are made at the nodes of a spatial network, which are sampling locations such as weather stations or traffic flow detectors. At each node an individual time series is collected that describes the temporal evolution of the space-time process at a single point in space.

A time series \(z=\{z(t)/z \in T\}\) in temporal domain T is a sequence of observations of a process taken at equally spaced time intervals: \(z_t, z_{t-1}, z_{t-2}, … z_{t-{(n-1)}}\), where \(z_t\) denotes the value of some quantity \(z\) at time \(t\) and \(n\) is the lengh of the serie. \(z_{t-{(n-1)}}\) indicates the time at which the first available observation was made (for further details, see Haworth 2013).

---

1.4 Forecasting Data and Methods

To model time series data we need to understand past behavior to project future values. We need to explore datasets characteristics in order to examine their attributes and evaluate the methods that would be applied.

1.4.1 Data Description

The traffic data used in this book are travel time times (TTs) provided by Transport for London (TfL) as part of the London Congestion Analysis Project (LCAP). To ensure accurate results with exploratory data analysis and predictive models, some links have been removed from the original dataset due to poor data quality⁴.

To visualize the London congestion analysis project road links we need to install the package tmap. Note that any package need to be installed first using the command install.packages('package_name') before it can be loaded using the command library(). Before a library is loaded its functions will be inaccessible, even if it is installed.

# install if necessary using the command 'install.packages'
library(tmap)

The package tmap (thematic map) creates a tmap-element that specifies a spatial data object, which we refer to as shape. tmap is a library that simplifies many of the elements of map creation. It uses the basic syntax style of the most popular graphics library in R.

# first, we need to load the data to the space environement
load("forecasting.RData") 

# the command 'tm_shape' is used to setup and display the map
bmap <- read_osm(LCAPShp, type="osm")
tm_shape(LCAPShp) +
  tm_lines(col="LENGTH", style="jenks", palette="Dark2", lwd=2.5)+
  tm_shape(bmap)+tm_rgb(alpha = 0.3)+
  tm_compass(position = c("left", "top")) +
  tm_scale_bar(position = c("right", "bottom"))+
  tm_layout(main.title="LCAP: subset of road links",
            frame.lwd = 4,
            inner.margins = 0.01,
            legend.position = c("left", "bottom"),
            legend.bg.color = "white",
            legend.frame = "black",
            main.title.color = "#382d2d",
            compass.type = "8star",
            main.title.position = c("center", "top"))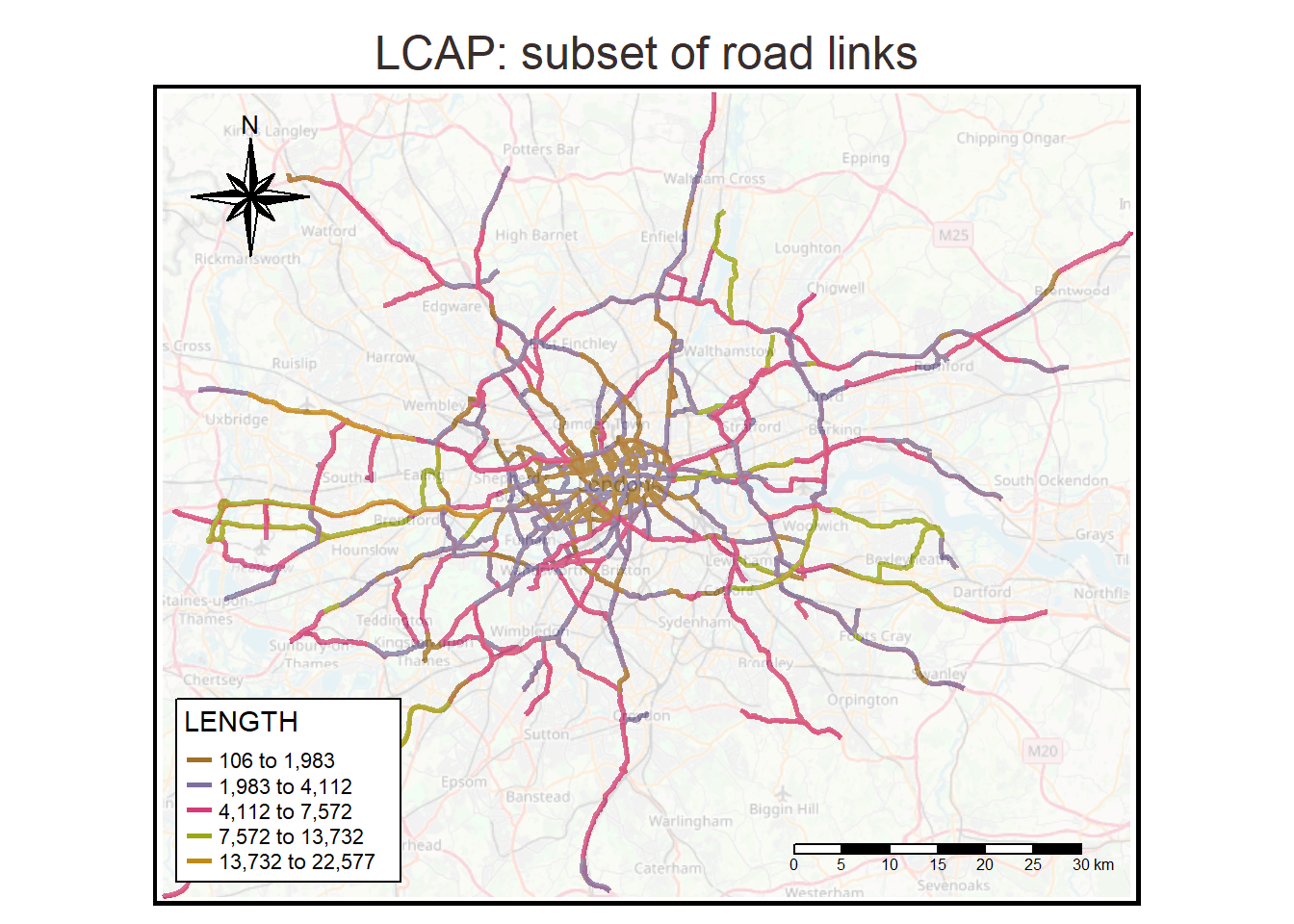

Figure 1.4: The London congestion analysis project road links

LCAP is a system of automatic number plate recognition (ANPR) cameras, maintained by TfL, that monitors London’s road network 24 hours a day. Link travel times of individual vehicles are recorded and aggregated at the 5 minute level, providing travel time information on all of London’s major roads with 288 observations per link per day.Figure 1.5 displays the main features of the monitor system.

Figure 1.5: Travel time data (source: adapted from Haworth 2013).

The TT of a vehicle can be defined as the time taken to travel between two fixed points, for example, between one intersection and the next, or between home and work. Formally, the TT of an individual vehicle can be expressed as:

\[\begin{equation} \operatorname{TT} = t_2 - t_1 \tag{1.5} \end{equation}\]

Where \(t_1\) is the time at which the vehicle began its journey and \(t_2\) is the time at which it completed its journey.

The road networks of major cities are equipped with sensor networks that measure traffic properties directly from traffic stream. The data used in the tutotial sections of this book were collected using automatic number plate recognition (ANPR) technology on London’s road. Each road link is paired with two ANPR cameras installed on the start and the end of the link. The first camera records the vehicle license plate and entrance time and the second camera records the exit time by matching the license plate. For this study individual TTs were aggregated at 5 minutes intervals giving 180 observations per day between 6am and 9pm. The travel time data is presented in unit travel times (second/metre).

1.4.2 Applied Methodologies

Quantitative forecasting can be applied when two conditions are satisfied:

1. numerical information about the past is available;
2. it is reasonable to assume that some aspects of the past patterns will continue into the future.

There is a wide range of quantitative forecasting methods, often developed within specific disciplines for specific purposes. Each method has its own properties, accuracies, and costs that must be considered when choosing a specific method.

When forecasting time series data, the aim is to estimate how the sequence of observations will continue into the future. To evaluate forecast accuracy it is common practice to separate the available data into two portions, training and test data. The training data is applied to estimate the parameters of the method and the test data is used to evaluate its accuracy.

Figure 1.6: Training Data.

The literature on space-time forecasting can be broadly separated into two categories: the statistical parametric framework and machine learninhg models.

Statistical parametric framework models are usually based on some form of autoregression (AR), whereby the current value of a series is modelled as a function of its previous values. The space-time autoregressive integrated moving average (STARIMA) is a widelly used parametric modelling framework for spatio-temporal data.

A parametric model is one where the functional form of the relationship between the dependent and independent variables is described by a set of parameter and for stationary time series in which there is no significant trend in the data over time. However, it is not unusual for time series data to exhibit some type of upward or downward trend over time, like trend and seasonability.

Trend: is the sweep or general direction of movement in a time series. It reflects the net influence of long-term factors that affect the time series in a consistent and gradual way over time (Hyndman and Athanasopoulos 2018).

Seasonality: a regular, repeating pattern in the data or the presence of variations that occur at specific regular intervals less than a year. For example, urban traffic usually shows the same patterns on working days: heavy traffic are expected in the morning and after working hours.

As more real world datasets become available at higher spatial and temporal resolutions, the task of describing space-time structures with conventional methods becomes more difficult. Non-parametrics methods as Machine Learning provides an alternative approach. ML models tend to be more complex black–box models that are created to maximize predictive accuracy. They are used to model complex, nonlinear, non-stationary relationships in massive, real world datasets.

Machine learning uses past data to make accurate predictions of future events. Learning refers to the iterative process of finding a classifier or regression algorithm with optimal solution by means of training data, and then to test simulation data under the same parameters. The general learning task is usually to find a mapping function between a limited set of input/output pairs \({(x_1, y_1, ..., x_n, y_n)}\), referred to as training data, where \(n\) is the number of training examples. This process is know as supervised learning. There are other strategies of learning, the principals can be described as follow:

• Supervised learning: given a set of labelled training data, a function is sought to predict labels for unseen data.
  • Examples: Regression (e.g. kernel ridge regression, SVR, ANNs); classification (for example SVMs, random forests, ANNs).
• Semi-supervised learning: small amount of labelled data, large amount of unlabelled data. Using both can improve predictions.
  • Examples: Generative models, low density separation and graphical methods.
• Unsupervised Learning: no labels are supplied with training data, and structure is sought.
  • Examples: clustering (k-means, hierarchical), dimensionality reduction (PCA), self-organizing maps, density estimation, data mining techniques.
• Reinforcement learning: a computer must perform a task in a given environment without knowledge of whether it has come close to its goal.
  • Examples: driverless cars, playing chess/Go against an opponent, DeepMind.

(source: Cheng and Haworth 2019)

The focus of ML is on generalisation, the ability of the algorithm to predict unseen data samples. It stands as a different approach of classical statistics, where the focus is on in-sample performance, and different to data mining which seeks to discover new knowledge from unlabelled data. ML does not assume that the functional form of the relationship between dependent and independent variables is known and can be described by model parameter. The technique minimizes error on unseen data, known as structural risk minimization, with no prior assumptions made on the probability distribution of the data.

The choice of method depends on the characteristics of the dataset. Modelling and forecasting of highly nonlinear, nonstationary and heterogeneous processes require models able to account for these properties. Table 1.3 and 1.4 outline the mains characteristics of each methology.

Table 1.3: Statistical parametric framework models

Technique	Main features
The space-time autoregressive integrated moving average (STARIMA)	STARIMA has been adapted from ARIMA models. It explicitly accounts for spatial structure in the data through the use of a spatial weight matrix.
Seasonal and Trend Decomposition using Loess Forecasting Model (STLF)	The STLF model comprises of a time series decomposition and a non-seasonal forecasting method. It decomposes the time series into a seasonal component, a trend-cycle or simply trend component, and the reminder component.

Table 1.4: Machine learning models

Technique	Main features
Support vector machine (SVM)	Makes use of the kernel trick to map the input data into a high dimensional feature space with a linear algorithm.
Kernel ridge regression (KRR)	Is a related Kernel method based on linear least squares regression.
Artificial neural networks (ANN)	The basic structure of an ANN is a layered, feed-forward, completely connected network of artificial neurons, termed nodes.

Machine learning uses past data to make accurate predictions of future events. Learning⁵ refers to the iterative process of finding a classifier or regression algorithm with optimal solution by means of training data, and then to test simulation data under the same parameters.

The focus of ML is on generalisation, the ability of the algorithm to predict unseen data samples. It stands as a different approach of classical statistics, where the focus is on in-sample performance and different to data mining which seeks to discover new knowledge from unlabelled data. ML does not assume that the functional form of the relationship between dependent and independent variables is known and can be described by model parameter.The technique minimizes error on unseen data, known as structural risk minimization, with no prior assumptions made on the probability distribution of the data

---

1.5 Chapter Summary

In this chapter, you have been introduced to modelling networks and forecast methods and principles. Forecasting models of network data have traditionally focussed on time series approaches. In such approaches, the network structure is ignored and each of the time series at the nodes is forecast independently.

Spatial network data combines the challenges of modelling time series and spatial series, which are autocorrelation, nonstationarity, heterogeneity and nonlinearity.

Many methods have been developed to model time series data. A common approach involves trying several modeling techniques on a given data set and evaluating how well they explain the past behavior of the time series variable. The most used accuracy measures are the mean absolute deviation (MAD), the mean absolute percent error (MAPE), the mean square error (MSE), ant the root mean square error (RMSE).

The literature on space-time forecasting can be broadly separated into two categories: the statistical parametric framework and machine learninhg models. The choice of method depends on the characteristics of the dataset. Modelling and forecasting of highly nonlinear, nonstationary and heterogeneous processes requires models that are able to account for these properties.

---

References

Borgatti, Everett, S. P., and J. C. Johnson. 2013. Analyzing Social Networks. Sage Publications.

Cheng, T, and J. Haworth. 2019. “Spatio-Temporal Data Analysis and Big Data Mining.” University College London.

Haworth, J. 2013. “Spatio-Temporal Forecasting of Network Data.” University College London.

Hyndman, R. J., and G. Athanasopoulos. 2018. Forecasting: Principles and Practice. OTexts.

Newman, M. E. 2003. “The Structure and Function of Complex Networks.” SIAM Rev 45(2): 167–256.

Ordnance-Survey. 2017. Integrated Transport Network Layer User Guide and Technical Specification. Vol. v1.0. Ordnance Survey - GB.

Wasserman, S., and K. Faust. 1994. Social Network Analysis: Methods and Applications. Cambridge university press.

Xie, F., and D. Levinson. 2007. Measuring the Structure of Road Networks. Geogr. Anal. Vol. 39(3).

---

4. A process known as data cleaning.↩

5. Learning machine is just another name for a family of functions \(f(x,α)\).↩